選用馬達：選用事例－分度盤機構
（1）驅動機構規格及使用條件
減速機型步進馬達非常適合大慣性慣量系統，例如分度盤。
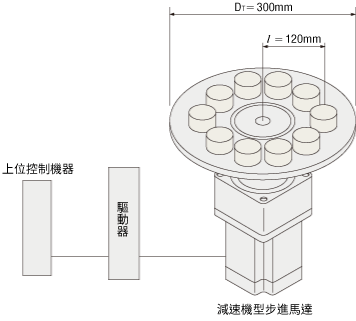
- 工作台直徑
- DT=300［mm］
- 工作台厚度
- LT=5［mm］
- 工作台材質
- 鋁（ρ=2.8×103［kg/m3］）
- 負載直徑
- DW=40［mm］
- 負載厚度
- LW=30［mm］
- 負載數量
- 10個（每36°排列）
- 負載材質
- 鋁（密度ρ=2.8×103［kg/m3］）
- 工作台中心到負載中心的距離
- l=120［mm］
- 位置定位角度
- θ=36°
- 定位時間
- t0=0.25秒
RKⅡ系列可使用PS減速機型（減速比36、解析度/脈波=0.02°）。
對於PS減速機型，慣性慣量驅動啟動/停止轉矩可使用瞬間最大轉矩
- 減速比
- i=36
- 解析度/脈波
- θS=0.02˚
（2）確定運轉模式
① 計算工作脈衝數A［脈波］
\(\begin{align} A & =\frac{\theta}{\theta_S} \\[ 5pt ]
& =\frac{36^\circ}{0.02^\circ} \\[ 5pt ]
& = 1800\ [\text{脈波}] \end{align}\)
② 確定加（減速）時間t1［s］
加減速時間以定位時間的25 %為宜。
然而，我們將使用t1=0.1［秒］。
③ 計算工作脈波速度f2［Hz］
\(\begin{align} f_2 & =\frac{A}{t_0 - t_1} \\[ 5pt ]
& =\frac{1800}{0.25 - 0.1} \\[ 5pt ]
& = 12000\ [\mathrm{Hz}] \end{align}\)
④ 計算運轉速度NM［r/min］
\(\begin{align} N_M & =\frac{\theta_S}{360^\circ} f_2 \cdot 60 \\[ 5pt ]
& =\frac{0.02^\circ}{360^\circ} \times 12000 \times 60 \\[ 5pt ]
& = 40\ [\mathrm{r}/ \mathrm{min}] \end{align}\)
（3）計算所需轉矩TM［N·m］
① 計算負載轉矩TL［N·m］
摩擦負載可以忽略不計，因此被省略。假設負載轉矩為0。
TL=0［N·m］
② 計算加速度轉矩Ta [N·m]
②-1 計算負載慣性慣量JL［kg·m2］
（公式請參閱I-4頁）
工作台面上慣性慣量
\(\begin{align} {J_T} & = \frac{\pi}{32} \rho\cdot{L_T}\cdot{{D_T}^4}\\[ 5pt ]
& = \frac{\pi}{32}\times\ 2.8 \times 10^3\ \times \left(5\times 10^{-3} \right)\times {\left(300\times 10^{-3} \right)}^4\\[ 5pt ]
& = 111.33 \times 10^{-4} \ [\mathrm{kg}\cdot\mathrm{m^2}]\end{align}\)
負載慣性慣量
（繞負載中心軸）
\(\begin{align} {J_{W1}} & = \frac{\pi}{32} \rho\cdot{L_W}\cdot{{D_W}^4}\\[ 5pt ]
& = \frac{\pi}{32}\times\ 2.8 \times 10^3\ \times \left(30 \times 10^{-3} \right)\times {\left(40\times 10^{-3} \right)}^4\\[ 5pt ]
& = 0.211 \times 10^{-4} \ [\mathrm{kg}\cdot\mathrm{m^2}]\end{align}\)
搬運重量
\(\begin{align} m_W & = \frac{\pi}{4} \rho\cdot{L_W}\cdot{{D_W}^2}\\[ 5pt ]
& = \frac{\pi}{4}\times\ 2.8 \times 10^3\ \times \left(30 \times 10^{-3} \right)\times {\left(40\times 10^{-3} \right)}^2\\[ 5pt ]
& = 0.106 \ [\mathrm{kg}]\end{align}\)
負載慣性慣量JW［kg·m2］相對於旋轉中心的距離可以用距離計算l［mm］負載中心與工作台旋轉中心之間、負載重量mW［kg］和負載慣性慣量JW1［kg·m2］繞其中心軸。
由於負載數量，n=10［pcs］，
負載慣性慣量
（繞著工作台中心旋轉）
\(\begin{align} {J_W} & = n \left( J_{W1} + m_W \cdot l^2 \right) \\[ 5pt ]
& = 10 \times\ \{ {\left(0.211 \times 10^{-4} \right)} + 0.106 \times {\left(120\times 10^{-3} \right)}^2 \}\\[ 5pt ]
& = 154.11 \times 10^{-4} \ [\mathrm{kg}\cdot\mathrm{m^2}]\end{align}\)
負載慣性慣量
\(\begin{align} {J_L} & = J_T + J_W \\[ 5pt ]
& = (111.33 + 154.11) \times 10^{-4} \\[ 5pt ]
& = 265.44 \times 10^{-4} \ [\mathrm{kg}\cdot\mathrm{m^2}]\end{align}\)
②-2 計算加速度轉矩Ta［N·m］
計算減速機出力軸的加速度轉矩。
\(\begin{align}T_a & = \frac{(J_0 \cdot i^2 + J_L)}{9.55} \cdot \frac{N_M}{t_1} \\[ 5pt ]
& = \frac{(J_0 \times 36^2 + 265.44 \times 10^{-4})}{9.55}\cdot \frac{40}{0.1} \\[ 5pt ]
& =54282.7 J_0 + 1.11\ [\mathrm{N} \cdot \mathrm{m}]\end{align}\)
用脈波速度計算加速度轉矩的公式如下。
計算結果是一樣的。
\(\begin{align}T_a & =(J_0 \cdot i^2 + J_L) \frac{\pi \cdot \theta_S}{180^\circ} \cdot \frac{f_2 - f_1}{t_1} \\[ 5pt ]
& =(J_0 \times 36^2 + 265.44 \times 10^{-4})\times \frac{\pi \times 0.02^\circ}{180^\circ}\times \frac{12000-0}{0.1} \\[ 5pt ]
& =54282.7 J_0 + 1.11\ [\mathrm{N} \cdot \mathrm{m}]\end{align}\)
③ 計算所需扭轉矩TM［N·m］
使用安全係數計算Sf=2。
\(\begin{align} {T_M} & = \left(T_L + T_a \right)S_f \\[ 5pt ]
& =\{ 0 + {\left(54282.7 J_0 + 1.11 \right)} \} \times 2 \\[ 5pt ]
& = 108565.4 J_0 + 2.22 \ [\mathrm{N}\cdot\mathrm{m}]\end{align}\)
（4）選用馬達
① 暫定選用馬達
| 品名 | 轉子慣性慣量［kg·m2］ | 必要轉矩 ［N·m］ |
|---|---|---|
| PKE543AC-PS36+RKSD503-AD | 30×10-7 | 2.55 |
② 從轉速－轉矩特性判斷馬達
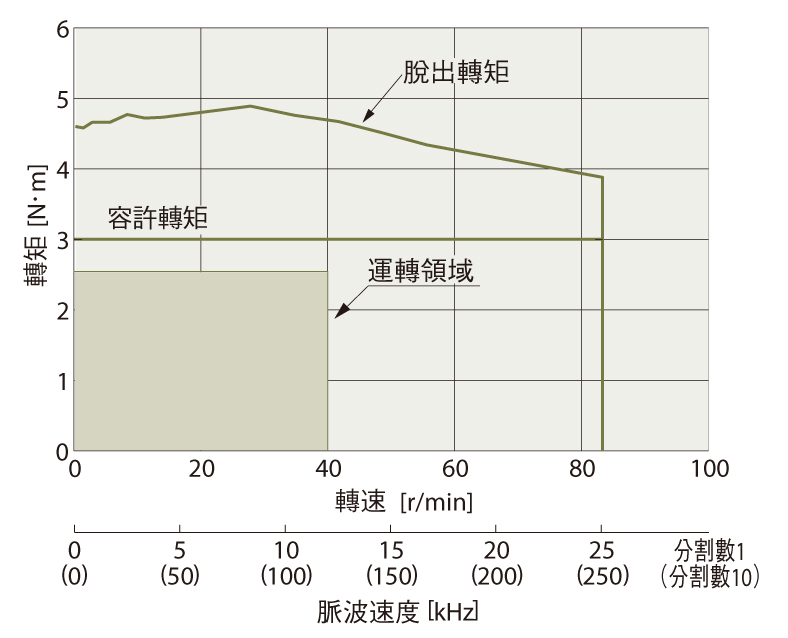
PS減速機型在負載慣性慣量啟動或停止時，可使用瞬間最大轉矩範圍的加速度轉矩。
由於馬達的工作區域（運轉速度和所需轉矩）落在轉速－轉矩特性的脫出轉矩內，因此可以使用該馬達。
檢查慣性慣量比，確保選用正確。
（5）檢查慣性慣量比
PKE543AC-PS36的減速比為36，因此慣性慣量比計算如下。
\(\begin{align} \frac{J_L}{J_0 \cdot i^2}
& = \frac{265.44 \times 10^{-4}}{30 \times 10^{-7} \times 36^2} \\[ 5pt ]
& \fallingdotseq 6.83\end{align}\)
PKE543AC-PS36馬達相當於PKE543AC馬達。由於慣性慣量比為30以下，因此如果慣性慣量比為6.83，則認為可以進行馬達動作。