選擇電動滑台/電動缸:負載慣量計算-電動滑台-
選用方法
負載慣量
當透過電動滑台輸送負載時,如果負載慣量的重心位置偏離工作台中心(支點),則負載力矩將作用在直線導軌上。
作用方向適用於3個方向:從OFFSET的位置往垂直方向(MP)、水平方向(MY)、滾動方向(MR)作用。
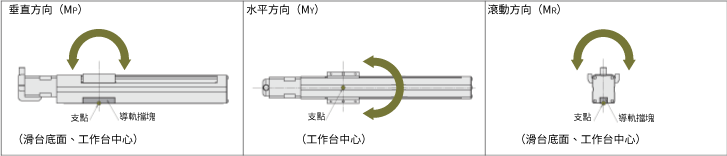
即使所選電動滑台符合搬運重量和定位時間要求,但當負載重心懸於工作台中心/出力軸導軌中心時,運轉壽命可能會因負載慣量而降低。必須完成負載慣量計算,並檢查條件是否在規格值範圍內。在靜態條件下施加的慣量為靜容許慣量。動態時施加的慣量為動容許慣量,兩者都必須檢查。
根據負載慣量和施加負載的方向計算施加於電動滑台的負載力矩。檢查靜容許慣量和動容許慣量是否在限制範圍內,並檢查強度是否足夠。
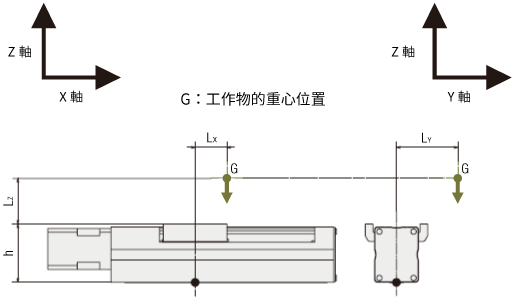
- m
- 搬運重量(kg)
- g
- 重力加速度9.807(m/s2)
- a
- 加速度(m/s2)
- h
- 電動滑台的工作台高度(m)
- LX
- X軸方向懸伸距離(m)
- LY
- Y軸方向懸伸距離(m)
- LZ
- Z軸方向懸伸距離(m)
- ΔMP
- 垂直方向的負載慣量(N·m)
- ΔMY
- 水平方向的負載慣量(N·m)
- ΔMR
- 滾動方向的負載慣量(N·m)
- MP
- 垂直方向的容許慣量(N·m)
- MY
- 水平方向的容許慣量(N·m)
- MR
- 滾動方向的容許慣量(N·m)
- 負載慣量判定公式:
\(\begin{align}\frac{|\Delta \mathrm{M_P}|}{\mathrm{M_P}} + \frac{|\Delta \mathrm{M_Y}|}{\mathrm{M_Y}} + \frac{|\Delta \mathrm{M_R}|}{\mathrm{M_R}} \leqq 1 \end{align}\)
當有多個懸吊載重時,由所有載重的慣量總和決定。
- 對於倍增負載(n個)
\(\begin{align}\frac{|\Delta \mathrm{M_{P1}} + \Delta \mathrm{M_{P2}} + \cdots \Delta \mathrm{M_{Pn}}|}{\mathrm{M_P}} + \frac{|\Delta \mathrm{M_{Y1}} + \Delta \mathrm{M_{Y2}} + \cdots \Delta \mathrm{M_{Yn}}|}{\mathrm{M_Y}} + \frac{|\Delta \mathrm{M_{R1}} + \Delta \mathrm{M_{R2}} + \cdots \Delta \mathrm{M_{Rn}}|}{\mathrm{M_R}} \leqq 1
\end{align}\)
負載慣量應用的概念
靜慣量應用的概念
下圖顯示了電動滑台的安裝方式和負載懸垂方式之間的組合的典型範例。選擇與您的使用條件相對應的範例之一。計算負載慣量(ΔMP,ΔMY,ΔMR)當電動滑台停止時,利用負載慣量判斷公式檢查是否在靜態容許慣量(MP,MY,MR)內使用。
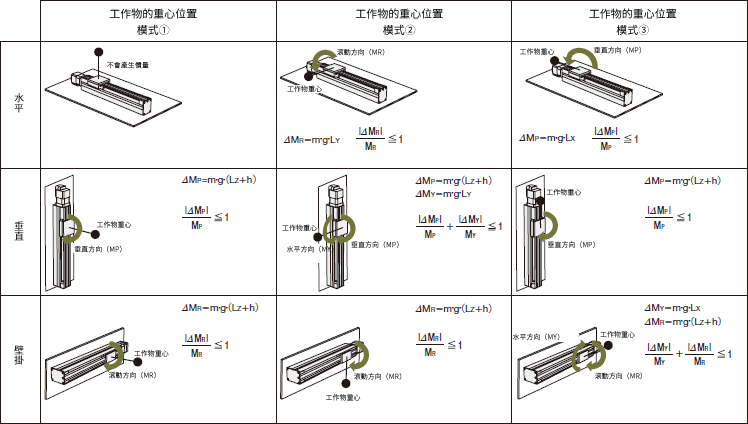
動慣量應用概念
下圖顯示了電動滑台的安裝方式和負載懸垂方式之間的組合的典型範例。選擇與您的使用條件相對應的這些範例之一。計算負載慣量(ΔMP,ΔMY,ΔMR)當電動滑台移動時(考慮加速度),利用負載慣量判斷公式檢查是否在動容許慣量(MP,MY,MR)內使用。
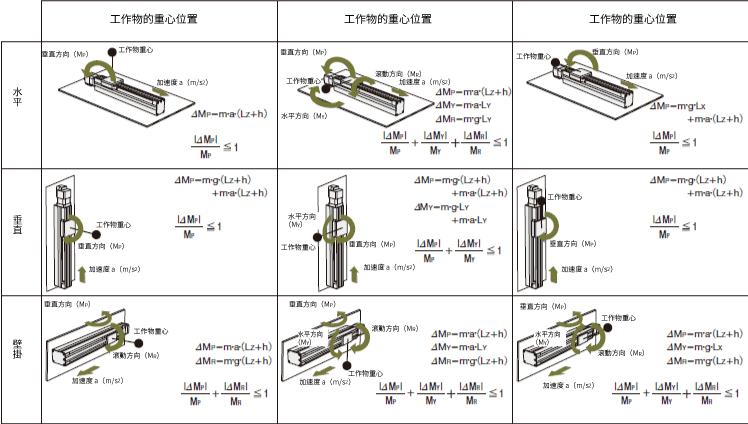
電動滑台的直線導軌的預期壽命距離是參考各系列的壽命而設計。
然而,在負載慣量公式大於1的情況下,預期壽命距離將小於預期值。
使用下面的公式來估算預期壽命。
\(\begin{align}
\text{預期壽命距離}(\mathrm{km}) = 5000 \mathrm{km^\ast}\times \left( \frac{1}{ \frac{|\Delta \mathrm{M_P}|}{\mathrm{M_P}} + \frac{|\Delta \mathrm{M_Y}|}{\mathrm{M_Y}} + \frac{|\Delta \mathrm{M_R}|}{\mathrm{M_R}}} \right)^3\end{align}\)
- *預期壽命因產品而異。詳情請參閱此處。